Performance Lab

Due date: Monday, Nov 24^th, 2025 @ 11:59pm PT

Notes

• This is an individual assignment – all code must be your own – no code sharing.
  It is fine to discuss optimizations with another student, but if you do, please write their name as a collaborator at the top of kernels.c.
• We made quite a few significant changes to the lab this year… apologies in advance for any problems.
• After you untar the lab download, please do not rename the folder name and keep it as “target-NUMBER”.
• Lab download / scoreboard website
• Lab TA: Chris

Lab Specific Rules (Please Please Read 🙏)

1. Please only run the lab on the cs33 servers (lnxsrv01, lnxsrv08, lnxsrv15).
2. Re-running your code won’t magically make it run faster. We’re using a CPU simulator to deterministically execute your code.
3. We tentatively grade you based on the local run you submitted. However, we will grade all the submissions independently after the deadline. If you don’t modify the grading script, you’ll get the same grade (i.e. it’s futile to spoof your grade).

Introduction

In this lab, your job is to optimize two simple “kernels” to make them faster and more energy efficient!

More specifically, given a suboptimal implementation of four kernels below, your goal is to utilize the optimization techniques you learned from class to speed up the calculation and improve “energy efficiency”. In this class, we approximate energy efficiency as the reduction in data movement across different levels of the memory hierarchy (i.e. so you should try to hit in the L1 cache as much as possible).

You’ll have to use some optimization techniques covered in the class, especially the cache and memory optimization ones.

Kernel #0: Compute absolute value (warm up)

Compute the element-wise absolute value of a 1D floating point vector.

Hints

• The control here is unpredictable, causing performance problems. Can you do this without control?
• Don’t worry about vector instructions for this one.

Kernel #1: 2D Transpose

In 2D transpose, we take a 2D input matrix (Ni by Nj), and swap its rows and columns to create a 2D output matrix (Nj by Ni).

We can define the transpose mathematically as follows:

Hints

• Think about the cache access pattern – it seems like we get bad spatial locality on either the In or Out array.
• Can we use tiling to help?
• Don’t worry about vector instructions for this one.

Kernel #2: Complex Matrix-Vector Multiplication

Here we are doing a matrix multiplication (similar to the one in class) but it will be complex matrix multiplication.

Hints

• The complex values are defined with a struct (see kernels.h). Think about the access pattern that is created when multiplying the values due to this struct.
• compArr is a global variable that does not change. Can you think of a way to reformat this into a new datastructure to avoid the nasty access pattern?
• Specifically you can use the init() function to preprocess the compArr, and feel free to add global variables.

Kernel #3-5: 3D Stencil

Stencil algorithms “apply” a stencil (sometimes called a filter) to an input array to produce an output array. Stencil methods are quite common in image processing and computer simulations.

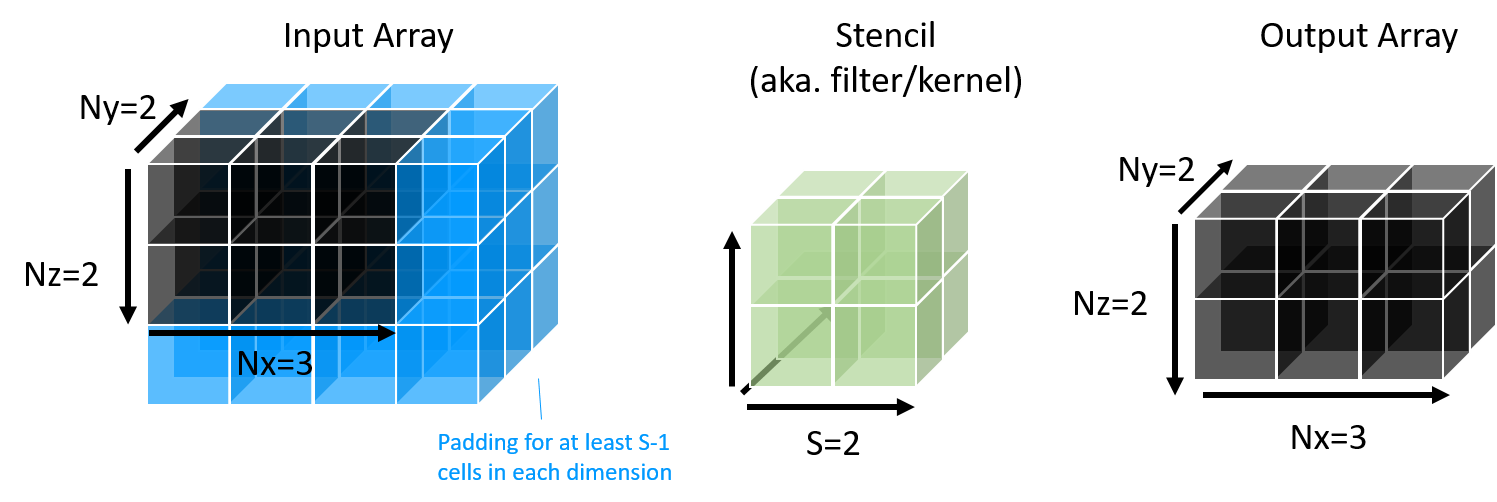
This stencil algorithm involves 3 arrays:

• “Input”: This is a large 3D array of input floating point values, with dimension sizes Ni, Nj, Nk. It has some padding in each dimension, based on the size of the Stencil array.
• “Stencil”: This is a smaller array of floating point values, with size S in all dimensions, which gets shifted over the input.
• “Output”: This is the same size as the input array, but without padding.

Below is a visualization of the three arrays involved:

Intuitively, the stencil algorithms shift the stencil around to every position on the input grid. For each position, we perform a dot product of the cells of Stencil and Input, and this result is written in the corresponding position of the Output array.

In this lab, we’ll define the 3D stencil for each cell of the output as follows:

Below we depict the computation process required for the first three pixels along the x dimension.

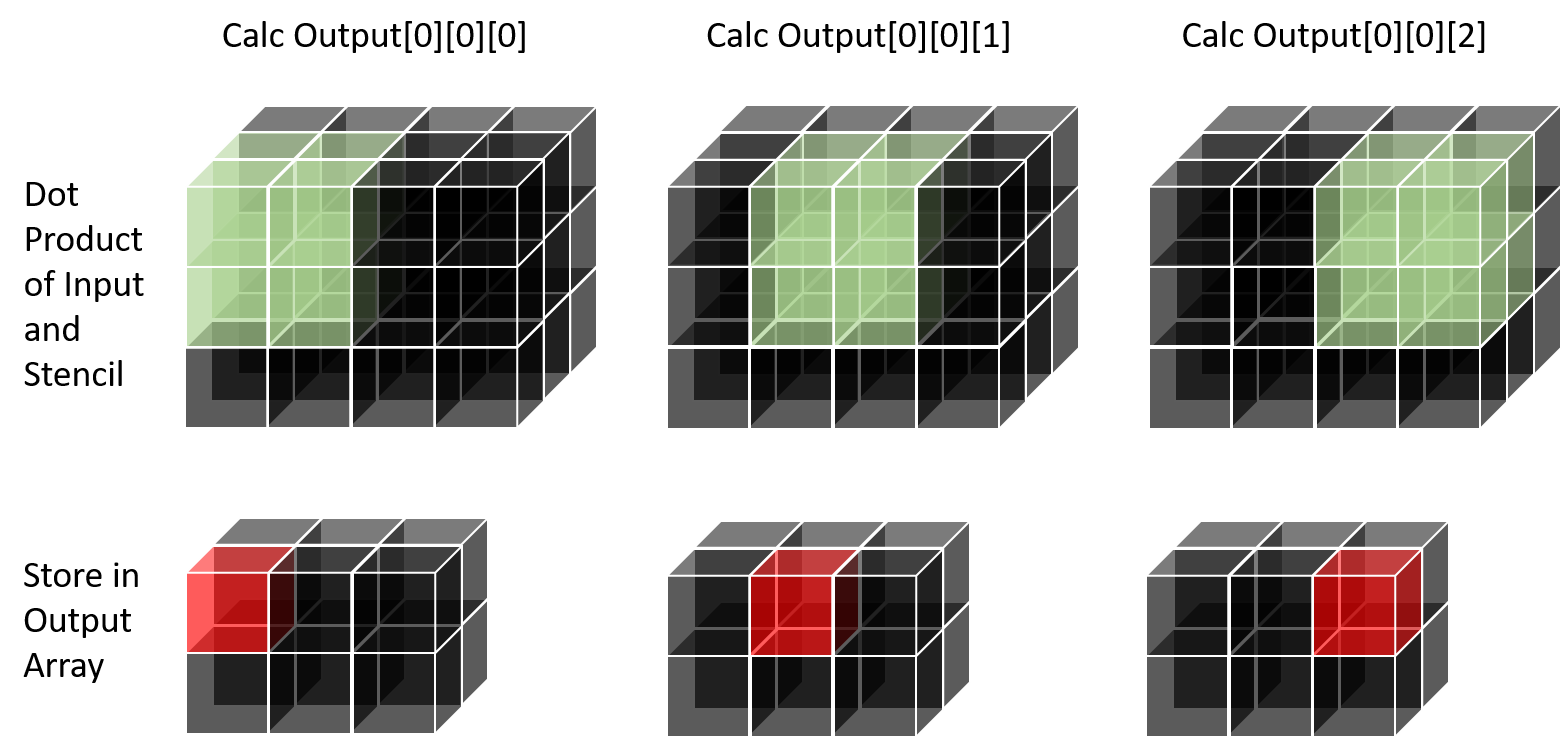
Note that there is significant data-reuse between different computations. The stencil values are reused completely at each iteration. On the second step (for $Output_{0,0,1}$), half of the cells used in the first step are reused.

Hints

• Create a distinct version of the code specifically for each problem size (Ni,Nj…). You may assume the problem sizes don’t change. When more of the variables are constants, the compiler can generate more efficient code.
• There is so much reuse that tiling is not so important here. For workload 5, however, there is an opportunity to tile.
• The loop ordering matters a lot, though. We really need to order the loops to get good temporal and spatial locality.
  • It will help you play with the loop ordering if you zero-out the Output array in a separate loop.
• GCC is definitely capable of vectorizing this code. Make sure that the statistics indicate that you are executing vector instructions – if not, your inner loop might not be chosen well to get contiguous access.

Scoring your Performance / Energy

For performance, we measure execution time. For energy efficiency, we are approximating it with “memory energy” for simplicity. Specifically, we use run your program with performance counters, and then multiply each access to L1/L2/L3 and DRAM by a somewhat arbitrary constant. The memory energy is defined as:

To get your final score, we will run your code with 4 different sets of matrix sizes. Test case 1 is for transpose, and test cases 2-4 are for stencil. To combine your performance and energy scores into a single metric, we first take the geometric mean of your performance and energy improvement scores. Then we compute “delay-energy improvement”, which multiplies your geometric mean performance and energy benefit together:

We will use the Delay-Energy improvement to calculate your score according to the following cutoffs (note the opportunity for extra credit):

• Delay-Energy Improvement == 1.5 -> Grade = 60
• Delay-Energy Improvement == 2.5 -> Grade = 70
• Delay-Energy Improvement == 12.5 -> Grade = 80
• Delay-Energy Improvement == 17.5 -> Grade = 90
• Delay-Energy Improvement == 30 -> Grade = 115

For reference, the TA solution achieves an delay energy improvement of 71.

Rules

1. All of your code should be in kernels.c. Any changes to the Makefile will be ignored. Do not rename any files.
2. You may not write any assembly instructions.
3. You may not use malloc or other alloc.
4. No external libraries may be used in kernels.c. (you can write your own functions of course). This also means you shouldn’t fork around.
5. Please no hacking the server! We are trusting you enough to run your code, so please be nice. It is not an achievement to hack someone when they let you run your own code 😝.

Downloading and running the Lab

You can only use the cs33 lnxsrv machine to edit your files (i.e. keep using cs33.seas.ucla.edu with VScode).

Step-1: Go to the lab website on your browser. Click into the “Request Lab” button on the webpage, insert the requested information to get a tarball. Then Secure copy(upload) the tarball from your local machine to the seas machines(using scp command on the command line or using other file transfer tools such as CyberDuck). In the terminal you can do the following:

scp <yourlocalfile> <yourusername>@cs33.seas.ucla.edu:~/<yourdir>

Alternatively, you can log into the cs33 server and download it with this command (substituting YOURUID and YOUREMAIL)

curl -X POST -d "uid=YOURUID&email=YOUREMAIL" -H "Content-Type: application/x-www-form-urlencoded" -O --remote-header-name "http://lnxsrv08.seas.ucla.edu:18213/get-tar-file"

Step-2: Log onto the cs33 server either using a terminal or your favorite text editor (VScode, etc), then go into the directory where the tarball was uploaded. Then untar the tarball. Note: YOURNUMBER should be replaced with the actual number assigned to your tarball.

ssh <yourusername>@cs33.seas.ucla.edu
tar -xzf target-YOURNUMBER.tar.gz 
cd target-YOURNUMBER

Step-3: Now you can start optimizing the code contained in kernels.c. Once you’re done optimizing, you can check the correctness and the performance of you code by compiling your code and running the following commands:

make 
./perflab.py

Make sure not to type “make perflab.py” or “make ./perflab.py” all one one line, because this will cause you to not compile everything (there’s another binary called “plain” that needs to get compiled as well).

You can also run a specific test input by passing the kernel test number (e.g. test 2)

./perflab.py 2

The lab will generate a report for you that indicates your performance.

Kernel tests and parameters:

# Kernel  |   Ni   Nj   Nk S 
----------+------------------
0 Abs     | 2048    1    1 1 
1 Transp. |  300  300    1 1 
2 MatVec  |  100  100    8 1 
3 Stencil |   16   16   16 4 
4 Stencil |   14   14   14 6 
5 Stencil |    4    4 1024 2 

Step-4: In order to be graded, you need to submit your work to the grading server, to do so, simply do:

make submit

The script will run it locally, before sending the results to the server. When we finalize your grade, we’ll re-run your submission with our copy of the grading script (our script is identical to yours).

Note:

1. If you want a comment to be shown on the scoreboard, you can write your comment in the comment.txt file, please keep it below 25 characters. If you attempt to insert a super long string, that will be rejected by the server.
2. We will count your best submission for your grade. You can submit multiple times, and we will take your best one. The score on the scoreboard is the score you will get (unless we found you didn’t follow the rules).
3. Make sure you save your progress often, things can go wrong at any time, you always want to have a backup of previous editions of your code. Check out version control tools, such as Git.

Interpreting Output

After you optimize your code a bit, you might see the following output:

# Kernel  |   Ni   Nj   Nk S |  Cycles     CPE #InstPE #VecInstPE |  L1 MKPE  L2 MKPE  L3 MKPE | Cycle Imprv. Energy Imprv.
----------+------------------+------------------------------------+----------------------------+---------------------------
0 Abs     | 2048    1    1 1 |    9836    4.80   3.029      0.001 |    503.4     64.9     64.0 |         3.68          2.68
1 Transp. |  300  300    1 1 | 2324465   25.83   5.637      0.000 |    278.3    230.7     31.3 |         1.13          3.16
2 MatVec  |  100  100    8 1 |  576534    7.21   4.939      2.215 |    616.4     63.9     63.8 |         2.99          2.83
3 Stencil |   16   16   16 4 |  641173    2.45   1.877      1.008 |    132.2     18.5      2.8 |         6.24         10.64
4 Stencil |   14   14   14 6 |  782515    1.32   2.577      1.215 |     53.0      8.2      1.1 |        11.27         12.17
5 Stencil |    4    4 1024 2 | 2084105   15.90   4.558      1.002 |    764.9    164.8     20.1 |         2.00          5.28

Overall Results:
 - Cycle Geomean:    3.47
 - Energy Geomean:   5.04
 - DelayEnergy:     17.49
 - Grade:           89.97

The table displays the following results

• # – Workload number
• Kernel – Kernel name
• Cycles – Total execution time in cycles
• CPE – Cycles Per Element
• #InstPE – Instructions Per Element
• #VecInstPE – Total SIMD/Vector Instructions Per Element
• #L1/L2/L3 MKPE – Number of L1/L2/L3 Misses Per one thousand Elements
• Cycle Imprv. – Speedup of your program compared to the original code
• Energy Imprv. – Energy Improvement of your program compared to the original code

We’ll also show the grading criteria and grade.

Hints and Advice

Things you should do for sure, and like right away:

• Inline all the functions! This reduces function call overhead, and enables the compiler to reason about the program region.
• Create a special version of each kernel that is specific to the matrix dimensions in each test case. This has two benefits: the compiler can create simpler code because it knows what the matrix dimensions are, and you can also optimize for each kernel differently. E.g. in the compute_stencil function, check the input arguments to see if it matches one of the test cases, then call a version specific to that test case.
• Try different loop orderings. Think about which ordering gives you the best spatial locality. Spatial locality is good for cache performance and the compiler will naturally vectorize loops with good locality.
• You can also try adding the “restrict” keyword in the first (outer) dimension of your array – this tells the compiler that the corresponding memory arrays don’t overlap, and could make the compilers job easier. I’ve seen this help a little on a couple of the stencil cases.
  • Syntax: func(float a[restrict N][N][N] ...)

General Advice:

• Every time you try something, check the stats (#instructions, cache accesses, etc.). See if what you did makes sense in the context of those stats – that will help you build up an understanding of what is working and why. I.e. I did loop tiling, and the number of L2 cache accesses went down because there’s better spatial locality for L1. (or maybe it didn’t go down, meaning you didn’t tile correctly, or the tiling size is wrong, etc.)

• Sometimes, simpler is better for the compiler.
  • Some optimizations can be done effectively by the compiler, so you should only do those yourself in the code if the compiler is not doing a good job. I.e. if you try something and it doesn’t help, then roll back and keep the simpler version! (PLEASE don’t show us your ugly code, that will make us very sad.)
  • E.g. we showed you how to unroll, use separate accumulators etc… but the compiler is like, realllly good at these most of the time. Sometimes, unrolling can make things worse for the compiler because the code gets more complex.
  • Overall, don’t forget to simplify when your optimizations don’t work. As Donald Knuth said, “Premature optimization is the root of all evil in programming.”

• Sometimes a recommended optimization (i.e. in the hints section) may slightly lower the performance for a particular case. This doesn’t mean it’s a bad optimization, it just means there was some interaction with your program and the compiler, or maybe there was some performance variability between runs. Keep going and implement the rest of the suggested optimizations, and you will get a good score. Also, you may need to play with the parameters of the optimization for it to work well (e.g. tile size).

• Start early, so you have enough time to finish and submit to the server, as the deadline approaches, there will likely be much longer wait times for submission.

Things you could do but probably shouldn’t do unless you’re a stubbornly curious person and you have time to burn:

• Manually unroll the code and/or use manual accumulators because you think you know better than the compiler. (But maybe sometimes you accidentally get lucky and do help the compiler)

• Try to use tiling to improve temporal locality as well (for stencil I mean). Intuitively, tiling can prevent you from going down a really long dimension without getting any reuse in your caches. What should your tile size be? Try to calculate the size of all the data you access within some inner loops – make sure this is less than the cache size you are targeting.

• The compiler will try to vectorize your code, and it’s kind of interesting to see why it did or didn’t vectorize. You can dump the (ugly) vectorization report by passing the flag -fopt-info-vec-all to GCC when compiling stencil.c. There is a comment in the Makefile that points out where to add the flag. Just look for the line number of your loop to see if it got vectorized or not. Sometimes it might vectorize an outer loop.

• Go look at the generated code by opening up the assembly of kernels.o (it’s in the build/ folder) using objdump or gdb. You might find out that certain program transformations help the compiler generate better code. However, looking at the assembly for these programs at high optimization levels may drive you to madness. So really proceed with caution.

CPU Microarchitecture Parameters

We’re using gem5 to simulate a custom x86 out-of-order CPU.

It shouldn’t be necessary to know the specific CPU properties to get a good grade; however, it could be useful under some advanced optimizations, and also just for understanding your results in general.

Compute

The simulator supports SSE instructions. It’s possible to use a single SSE instruction to do four float operations.

Cache

The cache line size is 64 bytes. Here’s the size and associativity of the three levels of cache:

Level |    Size | Associativity
------+---------+--------------
L1    |   2 KiB |         2-way
L2    |   8 KiB |         8-way
L3    | 256 KiB |        16-way

Reference

Here’s the output for the TA solution.

# Kernel  |   Ni   Nj   Nk S |  Cycles     CPE #InstPE #VecInstPE |  L1 MKPE  L2 MKPE  L3 MKPE | Cycle Imprv. Energy Imprv.
----------+------------------+------------------------------------+----------------------------+---------------------------
0 Abs     | 2048    1    1 1 |   10215    4.99   3.019      0.501 |    504.4     65.4     63.5 |         3.54          2.68
1 Transp. |  300  300    1 1 | 1341860   14.91  10.551      0.000 |    638.5     75.0     31.3 |         1.96          5.01
2 MatVec  |  100  100    8 1 |  144469    1.81   1.178      0.526 |    122.4     17.0     17.0 |        11.92         10.42
3 Stencil |   16   16   16 4 |  238448    0.91   1.721      1.008 |    103.3      2.9      2.8 |        16.78         13.67
4 Stencil |   14   14   14 6 |  558086    0.94   2.558      1.215 |     36.4      4.1      1.1 |        15.80         12.29
5 Stencil |    4    4 1024 2 |  283532    2.16   1.548      0.938 |    237.9     31.9     20.1 |        14.73         15.98

Overall Results:
 - Cycle Geomean:    8.28
 - Energy Geomean:   8.49
 - DelayEnergy:     70.30
 - Grade:          115.00